Roots of Complex Numbers
What is the square root of a complex number? Complex numbers also have two square roots; the principal square root of a complex number z, denoted by sqrt(z), is always the one of the two square roots of z with a positive imaginary part. The square roots of a + bi (with b ≠ 0) are , where
and
where sgn is the signum function. This can be seen by squaring to obtain a + bi.
Here √a²+b² is called the modulus of a + bi, and the square root sign indicates the square root with non-negative real part, called the principal square root; also where z = a + bi.
Principal square root of a complex number
To find a definition for the square root that allows us to consistently choose a single value, called the principal value, we start by observing that any complex number x + iy can be viewed as a point in the plane, (x, y), expressed using Cartesian coordinates.
The same point may be reinterpreted using polar coordinates as the pair ), where r ≥ 0 is the distance of the point from the origin, and varphi is the angle that the line from the origin to the point makes with the positive real (x) axis. In complex analysis, the location of this point is conventionally written If
then we define the principal square root of z as follows:
The principal square root function is thus defined using the nonpositive real axis as a branch cut. The principal square root function is holomorphic everywhere except on the set of non-positive real numbers (on strictly negative reals it isn’t even continuous). The above Taylor series for √1+x remains valid for complex numbers x with |x| < 1.
The above can also be expressed in terms of trigonometric functions:
Formula Roots of Complex Numbers
De Moivre’s Theorem: Let z = r(cos(θ) + ısin(θ).Thenzn = [r(cos(θ) + ısin(θ)]n = rn(cos(nθ) + ısin(nθ), where n is any positive integer.
Roots Of A Complex Number: A complex number z = r(cos(θ) + ısin(θ) has exactly nnth roots given by the equation 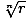 [cos(
[cos(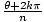 ) + ısin(
) + ısin(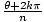 )], where n is a positive integer, and k = 0, 1, 2,…, n – 2, n – 1.
)], where n is a positive integer, and k = 0, 1, 2,…, n – 2, n – 1.
How do you find the square roots of a complex number?
Every complex number has complex square roots. However since we don’t know how to deal with expressions such as √i we need to follow a specific method to find the square roots of a complex number.
Let’s consider the complex number 21-20i.
We know that all square roots of this number will satisfy the equation 21-20i=x2 by definition of a square root.
We also know that x can be expressed as a+bi (where a and b are real) since the square roots of a complex number are always complex.
So 21-20i=(a+bi)2.
The natural step to take here is the mulitply out the term on the right-hand side.
This gives 21-20i=a2+(2ab)i+(b2)i2.
As i2=-1 by definition of i, this equation can be rearranged to give 21-20i=(a2-b2)+(2ab)i.
Now both sides of the equation are in the same form.
Let’s compare coeffiecients to obtain two equations in a and b.
First, let’s compare the real parts of the equation.
We have a2-b2=21 (call this equation 1).
Next, let’s compare the imaginary parts of the equation (the coefficients of i).
We have 2ab=-20 (call this equation 2).
We now have two equations in two unknowns. We can solve these simultaneous equations for a and b.
Firstly, we can make b the subject of equation 2 by dividing both sides by 2a.
We have b=-10/a.
Now substitute this expression for b into equation 1.
We have a2-(-10/a)2=21.
Some simplification and factorisation of this equation gives us (a2+4)(a2-25)=0, a quadratic in disguise.
So either a2=-4 or a2=25.
We have assumed a to be real so a2=-4 has no solutions of interest to us.
This means our solutions are a=5 and a=-5.
Substitute each a value into our earlier expression for b.
This means that when a=5, b=-2 and when a=-5, b=2.
So, putting a and b back into the context of the question, we have two solutions: 5-2i and -5+2i.
How to use this complex root calculator?
To use the complex root calculator, you can follow these steps:
- Enter the form of the complex number which you want to determine the complex roots of: you can choose between inputting it in its
Cartesian formor itspolar form. - Tell us the degree
nof the root you are interested in. - Our complex root calculator returns all
n-th roots of the number you entered. - You can choose the form in which the calculator displays the results (the Cartesian form or the polar form).
- If you need it, go to the
advanced modeto increase theprecision(number of decimal places) with which the complex root calculator displays its results. By default, we use4decimal places.
How to find complex roots by hand?
As for finding roots of complex numbers by hand, you can choose either an algebraic or geometric way. You can find both approaches below.
To algebraically find the n-th complex roots of a complex number z, follow these steps:
- If your number
zis given as its Cartesian coordinates,a + bi, convert it to the polar form. In other words, find its magnituderand argumentφ. - Compute the
n-th root ofr. - Compute
φ / nand its multiplicities:2 * φ / n,3 * φ / n, up to(n-1) * φ / n. - You can find the roots you’re looking for using the following formula
ⁿ√r * exp(i * (θ + 2kπ) / n)or, equivalently,ⁿ√r * (cos(θ/n + 2kπ/n) + i * sin(θ/n + 2kπ/n))where
k = 0, ..., n - 1.
To geometrically find all n-th roots of z, follow these steps:
- The first step is the same as in the algebraic approach: if your number is in its Cartesian form, compute its magnitude
rand argumentφ. - Plot a circle with a radius equal to the
n-th root ofr. All the roots we’re searching for lie in this circle. - On this circle, mark a point with argument
φ / n. This number is one of the roots and the starting point to find all the remaining ones! - Starting from this first root, make marks at every
2π / nradians until you make a full circle and come back to the starting point. These points are all the other complex roots you’re looking for.
Roots of Complex Numbers Exercises
1. Find the square root of 8 – 6i:
Answer:
Let z² = (x + yi)² = 8 – 6i
\ (x² – y²) + 2xyi = 8 – 6i
Compare real parts and imaginary parts,
x² – y² = 8 (1)
2xy = -6 (2)
Now, consider the modulus: |z|² = |z²|
\ x² + y² = √(8² + 6²) = 10 (3)
Solving (1) and (3), we get x² = 9 and y² = 1
x = ±3 and y = ±1
From (2), x and y are of opposite sign,
\ (x = 3 and y = -1) or (x = -3 or y = 1)
\ z = ± (3 – i)
2. Calculate: z = √(10-2i)
Answer:
z1 = √(10-2i) = 3.1778954-0.3146737i = 3.1934369 × ei (-0.0314165)
Complex number: 10-2i
Square root: sqrt (the result of step No. 1) = sqrt(10-2i) = √ 10-2i = 3.1778954-0.3146737i.
Related post: Complex Number | Addition, Subtraction, Multiplication, Division and Exercises
Sources: PinterPandai, Wikipedia












