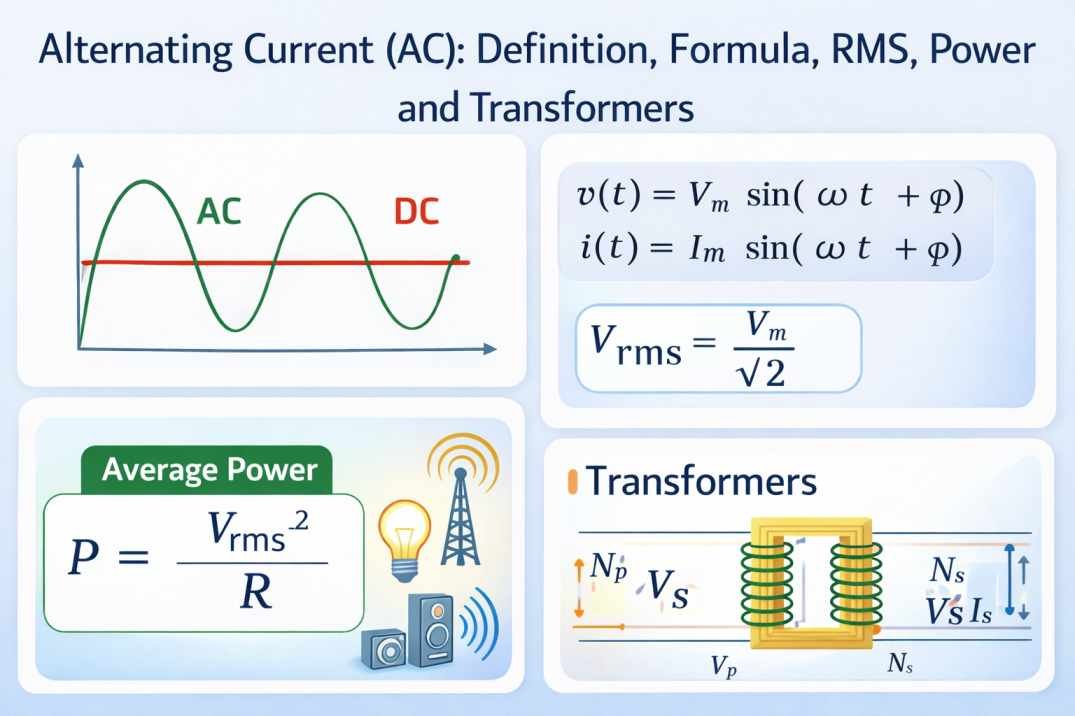
Roots of Complex Numbers and Exercise with Solution

cleverlysmart.com

3 years ago

Roots of Complex Numbers

What is the square root of a complex number? Complex numbers also have two square roots; the principal square root of a complex number z, denoted by sqrt(z), is always the one of the two square roots of z with a positive imaginary part. The square roots of $a + bi$ (with $b \neq 0$ ) are $<img decoding="async" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/fb2b47ea62c4c8da8a94f3d7529dbd64fc1f6aef" alt="\pm (\gamma +\delta i)" aria-hidden="true" width="4120.9" height="1223.9">$ , where

<img decoding="async" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/704c81398335c46acb3b42a729061750c766c45b" alt="\gamma ={\sqrt {\frac {a+{\sqrt {a^{2}+b^{2}}}}{2}}}" aria-hidden="true" width="9080.8" height="3304.9">

and

<img decoding="async" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/fd1eed684d46e10597454e9ef3bde6f4144739a6" alt="\delta =\operatorname {sgn}(b){\sqrt {\frac {-a+{\sqrt {a^{2}+b^{2}}}}{2}}}," aria-hidden="true" width="12705.8" height="3304.9">

where $sgn$ is the signum function. This can be seen by squaring $<img decoding="async" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/fb2b47ea62c4c8da8a94f3d7529dbd64fc1f6aef" alt="\pm (\gamma +\delta i)" aria-hidden="true" width="4120.9" height="1223.9">$ to obtain $a + bi$ .

Here √a²+b² is called the modulus of $a + bi$ , and the square root sign indicates the square root with non-negative real part, called the principal square root; also $<img decoding="async" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a88fbb46c61d4244904eb29921e3e9eeb26db234" alt="{\displaystyle {\sqrt {a^{2}+b^{2}}}={\sqrt {z{\overline {z}}}},}" aria-hidden="true" width="7691.8" height="1510.9">$ where $z = a + bi$ .

Principal square root of a complex number

To find a definition for the square root that allows us to consistently choose a single value, called the principal value, we start by observing that any complex number x + iy can be viewed as a point in the plane, (x, y), expressed using Cartesian coordinates.

The same point may be reinterpreted using polar coordinates as the pair $<img decoding="async" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b65d66a2ac837b13fce6c86289673cf4c44ed6d5" alt="{\displaystyle (r,\varphi }" aria-hidden="true" width="1940.7" height="1223.9">$ ), where r ≥ 0 is the distance of the point from the origin, and $varphi <img decoding="async" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/33ee699558d09cf9d653f6351f9fda0b2f4aaa3e" alt="\varphi " aria-hidden="true" width="654.5" height="936.9">$ is the angle that the line from the origin to the point makes with the positive real (x) axis. In complex analysis, the location of this point is conventionally written $<img decoding="async" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a4e3db48ba9cf6dac607fe95a0615e2caaf96333" alt="{\displaystyle re^{i\varphi }.}" aria-hidden="true" width="2003.6" height="1152.1">$ If

<img decoding="async" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/880753468cb5d28421f035236555ef024d6711e8" alt="z=re^{{i\varphi }}{\text{ with }}-\pi &lt;\varphi \leq \pi ," aria-hidden="true" width="11945.7" height="1367.4">

then we define the principal square root of z as follows:

<img decoding="async" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a1edff7851737fcd3646b9397a6ab44677ba42c2" alt="{\displaystyle {\sqrt {z}}={\sqrt {r}}e^{i\varphi /2}.}" aria-hidden="true" width="6181" height="1510.9">

The principal square root function is thus defined using the nonpositive real axis as a branch cut. The principal square root function is holomorphic everywhere except on the set of non-positive real numbers (on strictly negative reals it isn’t even continuous). The above Taylor series for √1+x remains valid for complex numbers x with |x| < 1.

The above can also be expressed in terms of trigonometric functions:

<img decoding="async" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3b1c6547d2ba001ee223f8823934863ace7496b0" alt="{\displaystyle {\sqrt {r\left(\cos \varphi +i\sin \varphi \right)}}={\sqrt {r}}\left(\cos {\frac {\varphi }{2}}+i\sin {\frac {\varphi }{2}}\right).}" aria-hidden="true" width="19436.4" height="2085">

Formula Roots of Complex Numbers

De Moivre’s Theorem: Let z = r(cos(θ) + ısin(θ).Thenzⁿ = [r(cos(θ) + ısin(θ)]ⁿ = rⁿ(cos(nθ) + ısin(nθ), where n is any positive integer.

Roots Of A Complex Number: A complex number z = r(cos(θ) + ısin(θ) has exactly nnth roots given by the equation 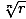[cos(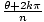) + ısin(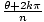)], where n is a positive integer, and k = 0, 1, 2,…, n – 2, n – 1.

Every complex number has complex square roots. However since we don’t know how to deal with expressions such as √i we need to follow a specific method to find the square roots of a complex number.

Let’s consider the complex number 21-20i.

We know that all square roots of this number will satisfy the equation 21-20i=x² by definition of a square root.

We also know that x can be expressed as a+bi (where a and b are real) since the square roots of a complex number are always complex.

So 21-20i=(a+bi)².

The natural step to take here is the mulitply out the term on the right-hand side.

This gives 21-20i=a²+(2ab)i+(b²)i².

As i²=-1 by definition of i, this equation can be rearranged to give 21-20i=(a²-b²)+(2ab)i.

Now both sides of the equation are in the same form.

Let’s compare coeffiecients to obtain two equations in a and b.

First, let’s compare the real parts of the equation.

We have a²-b²=21 (call this equation 1).

Next, let’s compare the imaginary parts of the equation (the coefficients of i).

We have 2ab=-20 (call this equation 2).

We now have two equations in two unknowns. We can solve these simultaneous equations for a and b.

Firstly, we can make b the subject of equation 2 by dividing both sides by 2a.

We have b=-10/a.

Now substitute this expression for b into equation 1.

We have a²-(-10/a)²=21.

Some simplification and factorisation of this equation gives us (a²+4)(a²-25)=0, a quadratic in disguise.

So either a²=-4 or a²=25.

We have assumed a to be real so a²=-4 has no solutions of interest to us.

This means our solutions are a=5 and a=-5.

Substitute each a value into our earlier expression for b.

This means that when a=5, b=-2 and when a=-5, b=2.

So, putting a and b back into the context of the question, we have two solutions: 5-2i and -5+2i.

How to use this complex root calculator?

To use the complex root calculator, you can follow these steps:

Enter the form of the complex number which you want to determine the complex roots of: you can choose between inputting it in its Cartesian form or its polar form.
Tell us the degree n of the root you are interested in.
Our complex root calculator returns all n-th roots of the number you entered.
You can choose the form in which the calculator displays the results (the Cartesian form or the polar form).
If you need it, go to the advanced mode to increase the precision (number of decimal places) with which the complex root calculator displays its results. By default, we use 4 decimal places.

How to find complex roots by hand?

As for finding roots of complex numbers by hand, you can choose either an algebraic or geometric way. You can find both approaches below.

With algebraic approach to finding roots of complex numbers

To algebraically find the n-th complex roots of a complex number z, follow these steps:

If your number z is given as its Cartesian coordinates, a + bi, convert it to the polar form. In other words, find its magnitude r and argument φ.
Compute the n-th root of r.
Compute φ / n and its multiplicities: 2 * φ / n, 3 * φ / n, up to (n-1) * φ / n.
You can find the roots you’re looking for using the following formulaⁿ√r * exp(i * (θ + 2kπ) / n)or, equivalently,ⁿ√r * (cos(θ/n + 2kπ/n) + i * sin(θ/n + 2kπ/n))
where k = 0, ..., n - 1.

With geometric approach to finding roots of complex numbers

To geometrically find all n-th roots of z, follow these steps:

The first step is the same as in the algebraic approach: if your number is in its Cartesian form, compute its magnitude r and argument φ.
Plot a circle with a radius equal to the n-th root of r. All the roots we’re searching for lie in this circle.
On this circle, mark a point with argument φ / n. This number is one of the roots and the starting point to find all the remaining ones!
Starting from this first root, make marks at every 2π / n radians until you make a full circle and come back to the starting point. These points are all the other complex roots you’re looking for.

Roots of Complex Numbers Exercises

1. Find the square root of 8 – 6i:

Answer:

Let        z² = (x + yi)² = 8 – 6i
\    (x² – y²) + 2xyi     = 8 – 6i
Compare real parts and imaginary parts,
x² – y² = 8                                      (1)
2xy = -6                                          (2)

Now, consider the modulus: |z|² = |z²|
\ x² + y² = √(8² + 6²) = 10 (3)

Solving (1) and (3), we get x² = 9 and y² = 1
x = ±3 and y = ±1

From (2), x and y are of opposite sign,
\ (x = 3 and y = -1) or (x = -3 or y = 1)
\ z = ± (3 – i)

2. Calculate: z = √(10-2i)

Answer:

z1 = √(10-2i) = 3.1778954-0.3146737i = 3.1934369 × ei (-0.0314165)

Complex number: 10-2i
Square root: sqrt (the result of step No. 1) = sqrt(10-2i) = √ 10-2i = 3.1778954-0.3146737i.

Sources: PinterPandai, Wikipedia