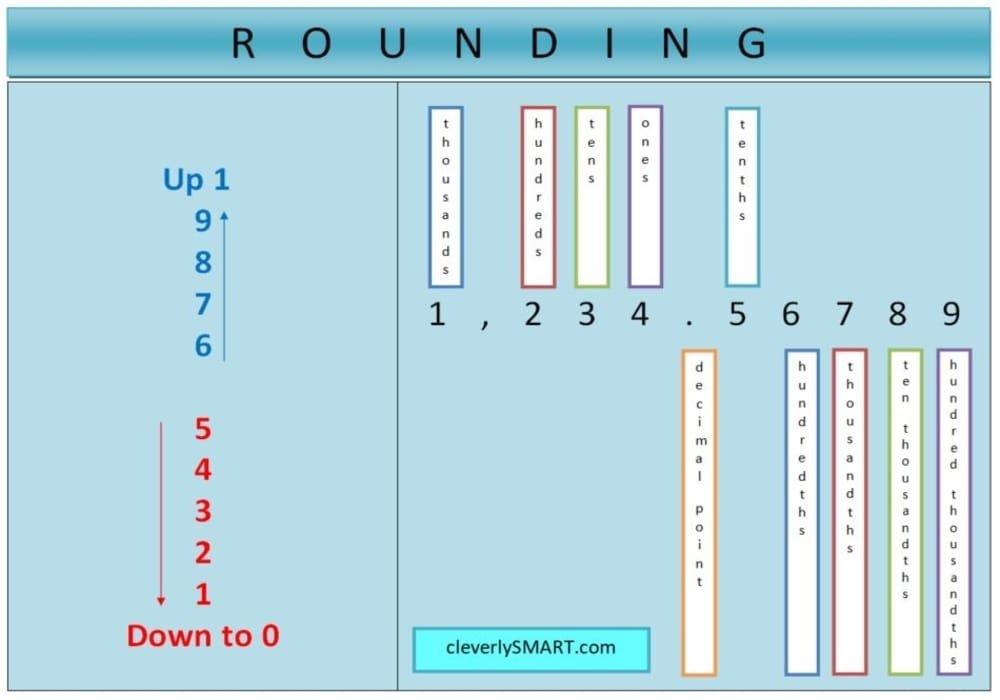
Rounding
Rounding numbers is important to generate numbers in mathematical calculations by producing a smaller number of digits.
Rules for Rounding Numbers
When rounding whole numbers there are two rules to keep in mind:
1. Find the digits for your rounding and look at the right side. If the digits are 0, 1, 2, 3 or 4, do not change the rounding number. All digits to the right of the required rounding digit will become 0.
2. Find the digits for your rounding and look to the right. If the digit is 5, 6, 7, 8 or 9, you can round the number by one number. All digits to the right of the required rounding digit will become 0.
Read also: Mean Mathematics | Examples, Questions and Answers
Rules for Rounding Decimal Numbers
When rounding decimal numbers, there are 3 rules to keep in mind:
Find your rounding number and look to the right side. If the number is 4, 3, 2 or 1, simply “drop” / round all digits to the right of it.
Find the digits for your rounding and look to the right. If the number is 5, 6, 7, 8 or 9 add one to the rounding number and “drop” / round all digits to the right of it.
Some teachers prefer this method: This rule provides more accuracy and is sometimes referred to as the “Banker Rule” (banking department). If the first digit dropped is 5 and there is no following digit or digit following a zero, make the previous number (even round to the nearest even number). For example, 2.315 and 2.325 are both 2.32 when rounded to the nearest hundredth order. Note: The reason for the third rule is that approximately half of the times will be rounded off and the other half of the time will be rounded.
Rounding to the nearest tens
Look at the hundredths digit (the digit after the tenths digit).
If it is less than 5 then round the number down by removing the decimal part of the number after then tenths digit;
if it is 5 or more then round the number up by adding one on to the tenths digit and removing the rest of the decimal part of the number.
Examples
1.6 = 2
1.16 = 1.2
1.25 = 1.3
1.76 rounds up to 1.8 because the hundredths digit is a 6.
8.746 rounds down to 8.7 because the hundredths digit is a 4.
14.252 rounds up to 14.3 because the hundredths digit is a 5.
Rounding To Nearest Hundreds
525 = 500
717 = 700
1,250 = 1,300
2,781 = 2,800
4,524 = 4,500
5,359 = 5,400
6,168 = 6,000 + 100 + 68 = 6,000 + 100 + 100 = 6,200
6,998 = 6,000 + 900 + 98 = 6,000 + 900 + 100 = 7,000
10,343 = 10,000 + 300 + 43 = 10,000 + 300 + 0 = 10,300
7,423 = 7,400
Rounding to Nearest Tens of Thousands & Hundreds of Thousands
58,943 = 50,000 + 8,943 = 50,000 + 10,000 = 60,000
350,165 = 300,000 + 50,165 = 300,000 + 50,000 = 350,000
123,965 = 100,000 + 23,965 = 100,000 + 20,000 = 120,000
668,265 = 600,000 + 68,265 = 600,000 + 100,000 = 700,000
247,625 = 200,000 + 47,625 = 200,000 + 50,000 = 250,000
Rounding Whole Numbers
The numbers can be rounded to the nearest ten, hundred, thousand, and so on.
When rounding a number, first identify the rounding digit. Then follow the following two rules.
(a)(a) If the number to the right of the rounding digit is 0,1,2,3, or 40,1,2,3, or 4 (that is, less than 55 ), then keep the rounding digit and change the rest of the digits right to the rounding digit to zero.
Rounding Decimals
First work out which number will be left when we finish.
Rounding to tenths means to leave one number after the decimal point.
Rounding to hundredths means to leave two numbers after the decimal point.
etc.
3,1416 rounded to hundredths is 3,14
as the next digit (1) is less than 5
3,1416 rounded to thousandths is 3,142
as the next digit (6) is more than 5
1,2735 rounded to tenths is 1,3
as the next digit (7) is 5 or more
To round to “so many decimal places” count that many digits from the decimal point:
1,2735 rounded to 3 decimal places is 1,274
as the next digit (5) is 5 or more
Rounding to Significant Digits
To round to “so many” significant digits, count digits from left to right, and then round off from there.
1,239 rounded to 3 significant digits is 1,24
as the next digit (9) is 5 or more
134,9 rounded to 1 significant digit is 100
as the next digit (3) is less than 5
When there are leading zeros (such as 0,006), don’t count them because they are only there to show how small the number is:
0,0165 rounded to 2 significant digits is 0,017
as the next digit (5) is 5 or more
Questions and Answers
1. Round 63 to the nearest 10
A. 50
B. 60
C. 65
D. 70
Answer:
• We want to keep the “6” as it is in the 10s position
• The next digit is “3” which is less than 5, so no change is needed to “6”
Answer: 60
(63 gets “rounded down” to 60)
2. Round off 975.6539 to the nearest whole number
Solution:
The number in the tenths place is 6. Add one digit to ones digit and drop all the numbers after the decimal point.
975.6539 → 976
3. Round 3.995 to 2 significant digits.
A. 3.9
B. 3.99
C. 4.0
D. 4
Answer:
3.995 has 4 digits, so we have to lose two digits.
The first digit we will drop (in the hundredths place) is a 9, which is 5 or more so the tenths digit (9) is rounded up to 10.
This means the 1 is carried to the next digit to the left (units digit) and the units digit (3) is increased to 4.
The result is 4.0
(Note: we don’t just write “4” because that is only 1 digit, and we were asked for 2 significant digits.)
4. Round off the following number to the nearest tenths: 845.324
Solution:
The hundredths digit is 2. Drop all the digits after hundredths place
845.324 → 845.30
5. Round 3.8439 to the nearest hundredth.
A. 3.84
B. 3.843
C. 3.844
D. 3.85
Answer:
• We want to keep the “4” as it is in the hundredths position
• The next digit is “3” which is less than 5, so no change is needed to “4”
Answer: 3.84
(3.8439 gets “rounded down” to 3.84)
Note that it doesn’t matter that there is a 9 in the ten thousandths position. What is important (in deciding whether to round up or down) is what digit is in the thousandths position – this is a 3, so we rounded down.
6. The length of a road is 27.56 km. What is the length to the nearest km?
Solution:
27.56 is rounded off to the nearest whole number.
27.56 → 28 km.
7. Round 95 to the nearest 10
A. 80
B. 90
C. 95
D. 100
Solution:
• We want to keep the “9” as it is in the 10s position
• The next digit is “5” which is 5 or more, so increase the “9” by 1 to “10”
That is 10 tens
Answer: 100
(95 gets “rounded up” to 100)
Here we have an example of having to round a 5. Remember that 5 is in the middle … so we could go up or down. However, we follow the common method of rounding a 5 up to keep the ‘teams’ equal.
8. The weight of a boy is 37.35 kg. Calculate the weight to the nearest kg.
Solution:
37.35 is rounded off to the nearest whole number as
37.35 → 37 kg.
9. Round 78.546 to two decimal places.
A. 78
B. 79
C. 78.54
D. 78.55
Solution:
The given number has three decimal places. The digit in the second decimal place is the 4.
• We want to keep the “4” as it is in the second decimal place
• The next digit is “6”, which is 5 or more, so increase the “4” by 1 to “5”
Answer: 78.55
(78.546 gets “rounded up” to 78.55)
10. Round 24.56 to 3 significant digits.
A. 2.456
B. 24.5
C. 24.560
D. 24.6
Solution:
24.56 has 4 digits, so we have to lose one digit.
The third digit is 5
The next digit (6) is 5 or more, so the third digit (5) is rounded up to 6.
So the answer is 24.6
11. Round the following numbers: 1.587954655255. Round to: nearest thousands, hundreds, tens!
Answer:
Thousands: 1,588
Hundreds: 1.59
Dozens: 1.6
12. Round the following numbers: 153,256,566,566. Round to: hundreds of millions: tens of millions, millions, hundreds of thousands, ten thousand, thousands, hundreds, tens of nearest!
Answer:
Hundreds of millions: 153,300,000,000
Ten million: 153,260,000,000
1 million: 153,257,000,000
Hundreds of thousands: 153,256,600,000
Ten thousand: 153,256,570,000
One thousand: 153,256,567,000
Hundreds: 153,256,566,600
Dozens: 153,256,566,570
Sources: PinterPandai, CalculatorSoup