Unit circle

The unit circle intersects with algebra (with the equation of the circle), geometry (with angles, triangles and the Pythagorean theorem) and trigonometry (sine, cosine, tangent) in one place.

The name makes it clear: the circle of the unit is a circle with radius r = 1, which for convenience is assumed to be centered at the origin (0,0). Note that we are talking about the two-dimensional case.

Angles and circle of the unit

The unit circle, or a circle of any radius, is a very convenient way to work with angles. Recall that the measure of an angle is proportional to the amount of the circumference of the circle that the angle spans.

For example, if an angle covers a quarter of the circumference and its origin is the same as the center of the circle, then the measure of the angle is a quarter of the measure of a full angle, that is 360/4 = 90° if measured in degrees, or 2π/4 = π/2 measured in radians.

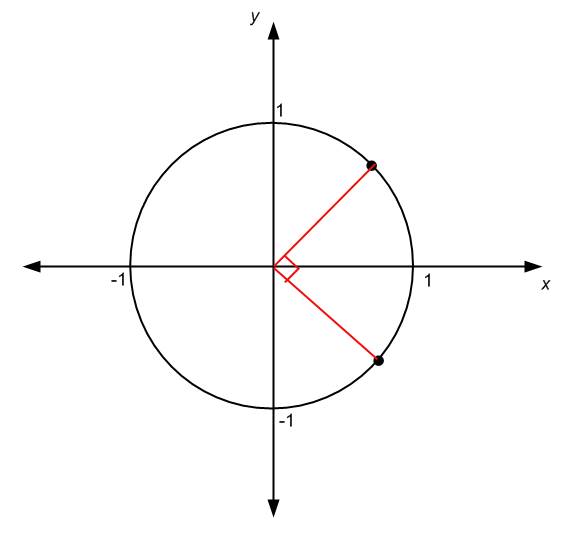
There are other circumstances in which the origin of the angle is not the same as the center of the circle, as in the case of the graphic below:

Trigonometric functions and circle of the unit

Using circle of the unit is very useful for working with trigonometric functions. Indeed, it turns out that if we have a point (x, y) in a circle of radius r, then we have this:

Sin α = y / r
cos α = x / r
tan α = y / r

where α is the angle shown in the figure below:

But when r = 1, i.e. when the radius is 1 (which is the case in the unit circle), we find that:

sin α = y
cos α = x
tan α = y / x

​

Therefore, the operation with trigonometric functions is much easier when the radius of a circle is 1, and then everything becomes much more visual. And we can use mnemonic rules like “the sine of an angle is the opposite side” and “the cosine of an angle is the adjacent side”.

The equation of the unit circle

The one who is centered at the origin, the equation that any point (x, y) on it satisfies is:

x² + y² = 1

Any pair (x, y) belonging to a circle of radius 1 must satisfy the above. If the point (x, y) does not satisfy the above, then it does not belong to the circle.

EXAMPLE 1

Does the point {(√2 / 2), (√2 / 2)} belong to the unit circle ?

Answer:

We need to check that the point satisfies the equation set above. On a:

x² + y² = {(√2 / 2)} ² + {(√2 / 2)} ² = 2/4 + 2/4 = 1

So in this case, the point {(√2 / 2), (√2 / 2)}

EXAMPLE 2

Does the point (1/2, 2/3) belong to the unit circle ?

Answer:

We need to check whether or not the point satisfies the equation set above. On a:

x² + y² = (1/2) ² + (2/3) ² = 1/4 + 4/9 = 25/36

So in this case, the point (1/2, 2/3) does NOT belong to the unit circle

Learn more about the circle of unity

One of the questions we always get is whether or not the unit circle equation describes a function. The answer is no. Indeed, the equation of circle of the unit rather defines a relation.

There are at least 2 ways to find out. The preferred test for students is the “vertical line test”. We have the following graph:

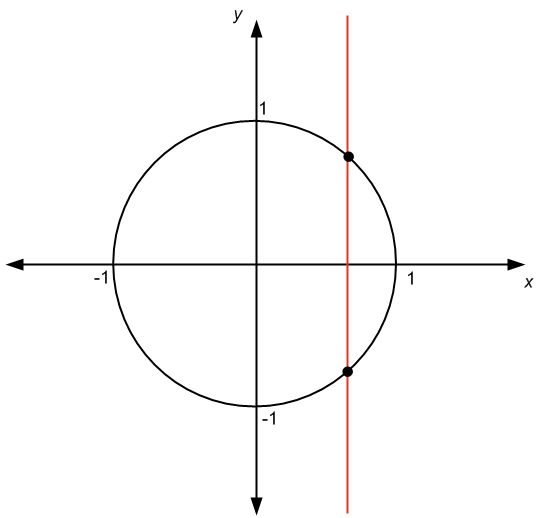
See in the graph above, and we can see that we have this vertical line crossing the graph at more than one point. The conclusion is that the graph represents a relation, not a function, now if you want to know what happens when the radius is not 1, and the circle is not centered at the origin.

The unit function and trigonometric functions

This is related to all trigonometric functions. The sine and cosine are directly represented by the sides of the triangles with vertices on the circle. In addition, measuring angles in radians makes a clear association with the angle and length of the generated arc.

Radians are the natural angle measurements for circles, although some people tend to feel more comfortable with degrees. Use this converting radians to degrees to make the desired conversions if you feel more comfortable with degrees instead of radians. What is radian? radian is the relationship that we say 2*π*r = 360 Degrees or that 1 Radian = 180/π Degrees and 1 Degree = π/180 Radians.

Read also: Function Mathematics (f) | Understand and use the concept of function

Sources: PinterPandai, Khan Academy, Pearson, NSCC Libraries Pressbooks

Photo credit: Jim.belk / Wikimedia Commons

Main photo explanation: showing the coordinates of certain points.