Fractions (mathematics)
Fractions, in mathematics, is naively a number of parts considered after dividing a whole number into equal parts. For example, the fraction 56/8 denotes the quotient of 56 by 8. It is equal to 7 because 7×8 = 56. In this fraction, 56 is called the numerator and 8 the denominator.
Numbers that can be represented by fractions of whole numbers are called rational numbers. The set of rationals is denoted Q.
There is a more general and more abstract definition of fractions. If (A, +, .) is an integral unitary commutative ring, we can create the field of fractions of A. Its elements are written (by analogy to fractions of integers) a/b and have the same operational properties (sum, product, simplification, …) as the fractions of Q.
How to calculate fractions easily
I – Sum and difference of fractions
When two fractions have the same denominator, we add or subtract the numerator and keep the denominator.
Example: 15/12 + 14/12 = 29/12 and 15/12 – 15/12 = 1/12
When two fractions don’t have the same denominator, we first make them have the same denominator and then add or subtract the numerator.
Examples:
15/4 + 11/16 = 15×3/4×3 + 11×2/6×2 = 45/12 + 22/12 = 67/12
15/4 – 11/6 = 15×3/4×3 – 11×2/6×2 = 45/12 – 22/12 = 23/12
II – Multiplication and division
To multiply two fractions, multiply the denominator and multiply the numerator.
Example: 5/8×7/12 = 5×7/8×12 = 35/96
Specifically, to multiply a fraction by a natural number, we simply multiply the numerator by this number and the denominator remains.
Example: 5/8×3 = 5×3/8 = 15/8
To divide by two fractions, multiply the first fraction by the reciprocal of the second fraction.
Example: 5/8 : 7/2 = 5/8×12/7 = 1×12/8×7 = 5×3/2×7 = 15/14
Franctions Exercises
1. Examples
2/3 +3/4 = 17/12
6/5+7/5 = 13/5
15/4 – 5/2 = 5/4
3/4 – 1/4 = 1/2
1/8 × 4/2 = 1/4
7/4 × 2 = 7/2
1/2 × 3/4 = 3/8
3/2 × 2 = 3
1/5 : 6/5 = 1/6
3/4 : 2/3 = 9/8
2/3 + 5/6 = 2×2/3×2 + 5/6 =4/6 + 5/6 = 9/6 = 3/2
2. Exercises on the rules for calculating fractions: we share a heritage. I take a quarter of it and my brother two-thirds of the rest. How much of the inheritance did my brother receive?
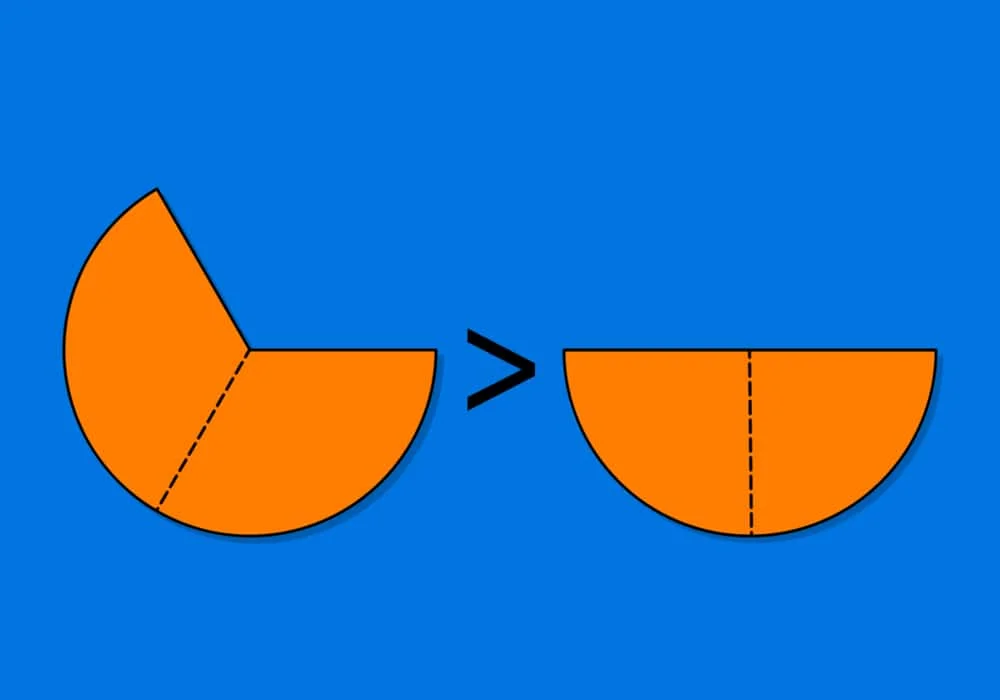
So my brother’s share corresponds to: 2/3 x 3/4 = 2/4 = 1/2 so, it means half of the total inheritance.
3. In a company there are 42 executives which represents 6/11 of the employees. How many employees are there in this company?
Answer:
We know what 6/11 represents, we are looking for how much the whole thing is 11/11 (or 1).
We will use the rule of three: we go back to the unit before going to calculate what we want.
If 6/11 is 42, then 1/11 is 6 times less so 7 (42÷6).
If 1/11 is 7, then 11/11 or the whole is 77 (11 times more)
So there are 77 employees in this company.
4. The box of chocolate that John bought contains 450 grams, he eats 5/9 of it. How many grams of chocolate did he eat?
Answer:
If the box of chocolate is divided into 9 equal parts and he takes 5 of those parts. Gold 450÷9 = 50 grams per slice. So 5 parts represent 250 grams.
Another method by applying the course on fractions:
John ate 5/9 of the 450 grams, hence the calculation is: 5/9 x 450
By calculating we get: 5/9 x 450=
5×450/9 = 5x9x50/9 = 5 x 50 = 250 grams
5. What is half of four-fifths of five-sevenths of 14?
Answer:
Keep in mind that “of” means “x” in a statement of fractions or percentages
We then obtain: (1/2 x 4/5 x5/7) x14 = 1/2 x (2×2/5) x 5/7 x 7 x 2=
2×2 = 4
6. If Anne drank 5/6 of a bottle that contained 1.8 liters of juice. How much juice, in centilitres, is left?
A) 10
B) 20
C) 18
D) 24
E) 30
Answer: E
If Anne has drunk 5/6 it means that there is 1/6 of the bottle left, i.e. 1/6 of 1.8 litres. It therefore remains to divide 1.8 by 6 which gives 0.3 liters or 30 cl.
7. Maria buys a package of 84 candies. She eats 3/7 the first day and then a third of the rest the next day. How many candies will she still have two days later?
A) 14
B) 18
C) 28
D) 32
E) 35
Answer:
Corrected exercise 6 on fractions: Answer D
If she eats 3/7 on the 1st day, she has 4/7 left. Let’s then calculate 4/7 of 84 to know the number of candies remaining after the 1st day. To do this, we divide 84 by 7 before multiplying by 4. We know that 12×7=84. So 84÷7=12. And 12×4=48.
So after the 1st day, he has 48 candies left. If she then eats 1/3 of these 48, it means that she has 2/3 left, i.e. 2/3 of 48. We proceed in the same way: 48÷3=16 and 16×2=32.
She will have 32 candies left on the 3rd day.
8. Michael spends half of his pay on his mortgage and then a third of the rest for his various bills. He then has 900 euros left. How much is his salary?
A) €1,800
B) €2,400
C) €2,700
D) €3,600
E) €4,500
Answer:
The key is to understand what fraction represents this €900?
After the credit, if he spends 1/3 of the rest on bills, he keeps 2/3 of the rest. But at this stage the remainder is 1/2 (half) of his pay.
So these €900 represent 2/3 of 1/2 or = 2/3 x 1/2 = 1/3 of all his pay (simplifying by 2). To determine his entire salary, we therefore multiply by 3, which gives €2,700.
9. A master chocolatier makes three types of chocolate: milk, dark and praline. Last week of all the chocolates sold, 2/7 were milk, 1/3 dark and 96 pralines. How much chocolate did he sell last week?
A) 192
B) 205
C) 224
D) 240
E) 252
Answer: E
In this type of question, we calculate the share, in fraction, that these 96 pralines represent before performing a rule of three to determine the total.
Let’s calculate milk + dark and then determine the remainder: 2/7 + 1/3 = 6/21 + 7/21 = 13/21. The rest is therefore what represents 96 chocolates. We will calculate what represents 1/21 before calculating the whole 21/21 = 1.
If 8/21 represents 96, then 1/21 represents 8 times month or 12 (in fact 8 × 12 = 96).
And therefore, it represents 21 times more or 21×12=252 chocolates in total.
10. In an election, Patrick received 3/10 of the votes in the first round. What fraction of the remaining votes must he obtain to have half of all the votes?
A) 1/5
B) 2/7
C) 3/10
D) 7/20
E) 1/2
Answer: B
The difficulty was to fully understand the question. Patrick got 3/10 of the votes, so there are 7/10 left. We are looking for what fraction of 7/10 must he obtain so that all his votes are 1/2. Keep in mind that “de” means “×”.
Method 1 of corrected exercise 9 on fractions:
The fastest was to dissect the problem. He currently has 3/10 of the votes and he wants 1/2, let’s first determine the part of the votes he lacks, 1/2 – 3/10 = 5/10 – 3/10 = 2/10 = 1/5. It must therefore obtain 1/5 of all the votes (and not the remainder) to have a majority.
Now we wonder what fraction of the remaining votes gives 1/5? That is, which proposition × 7/10 is 1/5. We test them:
A) 1/5 × 7/10 = 7/50 is not equal to 1/5
B) 2/7 × 7/10 = 2/10 and simplifying by 2 it gives 1/5.
Method 2 of corrected exercise on fractions:
we set the equation.
Let x be the desired fraction, we must solve: 3/10 + x X 7/10 x = 1/2
x X 7/10 = 1/2 – 3/10
or again: x X 7/10 = 1/5
and therefore: x = 1/5 x 10/7 = (1x2x5 / 5×7) = 2/7
Read also: Hardest Math Quiz
11. A florist has 411 roses and 685 Columbines. In order to prepare bouquets, he wishes to distribute these flowers by using them all and obtaining the maximum number of identical bouquets.
A) Calculate the number of bouquets.
B) Calculate the number of roses and lily in each bouquet.
1. The florist must use all the flowers and make a maximum of identical bouquets, the number of bouquets is therefore the GCD (Greatest Common Divisor) of 411 and 685. Using the method of successive Euclidean divisions we obtain:
685 = 411 x 1 + 274
411 = 274 x 1 + 137
274 =137 x 2 + 0
The GCD of 685 and 411 is the last nonzero remainder, so it’s 137.
The florist can therefore prepare 137 identical bouquets.
2. We have 411/137 = 3 and 685/137 = 5
Each bouquet is composed of 3 roses and 5 lilies.
Sources: PinterPandai, Davenport University, CueMath, MathIsFun
Photo credit: Ezra M. Katz (CC BY-SA 3.0) via Wikimedia Commons
