Fractal Geometry (Mathematics)

Fractional geometry, it deals with the fractional objects in metric spaces. A fractional object has an infinitely fragmented irregular spatial structure, and a topological dimension that is not necessarily an integer, unlike regular objects. A fractional object has a Hausdorff dimension greater than its topological dimension. A fractal object is a fractional object that also has a spatial structure that follows a deterministic or probabilistic rule involving internal self-similarity. Fractal geometry examines geometric fractal objects. This article looks at these geometries, and gives a list of practical applications, with a detailed case (Lorenz attractor).

The word “fractal” comes from the Latin “fractus” which means “broken”. Indeed, a fractal is an “infinitely fragmented” geometric object whose details are observable at an arbitrarily chosen scale.
By zooming in on a part of the figure, we can find the whole figure, we say that it is self-similar.

Although a number of things were already known, the discovery of fractals is attributed to a French polytechnician, Benoît Mandelbrot (1924; 2010).
His first research dates back to 1964 when he used the term self-similar in a study carried out at IBM. But it was in 1975 that he exhibited his work and gave the name “fractal” in his book “Fractal Objects”.

Fractals in many areas

Rough fractal shapes are easily seen in nature. The mathematical theory of fractals can provide interesting information in several scientific fields such as:

• in geology, relief study, coasts and watercourses, rock structures, avalanches;
• in animal morphology, invertebrate structures, bird feathers;
• in medicine, structure of the lungs, intestines, heartbeat;
• in meteorology, clouds, vortices, ice floes, rogue waves, turbulence, lightning structure;
• in volcanology, forecasting of volcanic eruptions, earthquakes;
• in astronomy with the description of the structures of the universe, craters on the Moon, distribution of galaxies;
• in human sciences, urban structure, evolution of demography;
• in economics, forecasting stock market crashes.

Simple and regular fractals with illustrations

Fractal	L system	angle	Distance ratio	Visualization	number of Mirror axes	Point symmetry	Rotational symmetry	Dimensions
Kite curve	F → R or F → L R → + R - L + L → -R ++ L-	45°	1: 1/√2		0	no	no	2
Gosper curve	F → R or F → L R → R + L ++ LR - RR-L + L → -R + LL ++ L + R - RL	60°	1: 1/√7		0	Yes	6 numbers	2
Hilbert curve	X X → -YF + XFX + FY- Y → + XF-YFY-FX +	90°	1: ½		1	no	no	2
Koch flake	F - F - F F → F + F - F + F	60°	1: ⅓		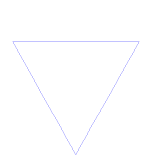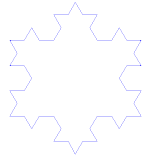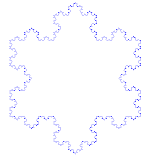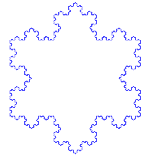12th	Yes	6 numbers	2
Peano curve	X X → XFYFX + F + YFXFY-F-XFYFX Y → YFXFY-F-XFYFX + F + YFXFY	90°			0	Yes	2 numbers	2
Peano curve	F. F → F-F + F + F + FFF-F + F	90°	1: ⅓		0	Yes	2 numbers	2
Penta Plexity	F ++ F ++ F ++ F ++ F F → F ++ F ++ F | F-F ++ F	36°	1: 1/{(√5+1) / (2)}²		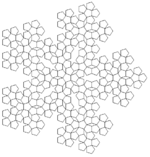10	no	5 numbers	2
Arrowhead	F → R or F → L R → -L + R + L- L → + RL-R +	60°	1: ½		1	no	no	2
Sierpinski triangle	FXF - FF - FF X → --FXF ++ FXF ++ FXF-- F → FF	60°			6th	no	3 numbers	2
Sierpinski triangle , 2nd variant	F - F - F F → F - F - F - ff f → ff	60°	1: ⅓		6th	no	3 numbers	2
Sierpinski carpet	F. F → F + FF-FF-FF-fF f → fff	90°	1: ⅓		8th	Yes	4 numbers	2
Levy C curve	F. F → + F - F +	45°	1: 1/√2		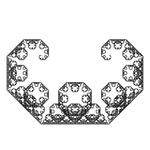1	no	no	2

Explanation of the L-system (Lindenmayer system)

The optional , i.e. not necessary, F is generally used as a route that is replaced by a sequence of instructions. Like the F , other capitalized letters such as R and L stand for a section of the route that is being replaced. + and – represent a specific angle that runs clockwise or counter-clockwise. The symbol | refers to a U-turn of the pencil, i.e. a turn by 180 °. If necessary, a corresponding multiple of the angle of rotation is used for this.

Example kite curve

 F → R
 R → + R - L +
 L → -R ++ L-

F is a simple distance between two points. F → R means that the segment F is replaced by R. This step is necessary because it has two recursive replacements, R and L, that contain each other. The following is replaced as follows:

 R.
 + R - L +
 + (+ R - L +) - (- R ++ L -) +
 + (+ (+ R - L +) - (- R ++ L -) +) - (- (+ R - L +) ++ (- R ++ L -) -) +
 .
 .
 .

From a certain section this replacement process has to be canceled in order to get a graphic:

 + (+ (+ r - l +) - (- r ++ l -) +) - (- (+ r - l +) ++ (- r ++ l -) -) +

Here, r and l each represent a fixed route.

Quiz Fractal

1. Fractals have become much more popular since the advent of electronic computing because they depend upon what aspects of computing?

a. the ability to rapidly create and graph large and complex sets of formuleic data
b. high levels of iteration and recursion
c. all of these
d. large numbers of calculations

Answer: all of these

Fractal problems have been touched upon since as early as the 17th century but most of the earliest work in the area was hindered by the amount of repetitive calculation that was required. In fact some of the earliest formulae in this area were referred to as mathematical “monsters” because of their unwieldiness.

2. Fractals are closely related to and often considered part of what field of Mathematics?

a. Combinatorics
b. Probability
c. Game Theory
d. Geometry

Answer: Geometry

Fractals are infinitely complex patterns that are self-similar across different scales The term “fractal” itself comes from the notion of breaking a line or a figure up into smaller but similar instances of the original. Conceptually, this is done over and over, ad-infinitum resulting in infinite sets.

Combinatorics deal primarily with counting and sets. Game theory deals primarily with strategies between rational decision makers (often in zero-sum games). Probability deals with the chances of indeterminate outcomes (e.g. odds & gambling)

3. What mathematician coined the word fractal and referred to himself on occasion as a “fractalist?”

René Descartes
Pierre de Fermat
Daniel Bernoulli
Benoit Mandelbrot
Answer:

Benoit Mandelbrot

Known for his talent for practical research, Mandelbrot and computer affinity, born a Polish Jew, became an IBM employee in 1958. He was one of the first to use computer graphics to create and display fractal geometric images which display “the art of roughness.”

4. Benoit Mandelbrot started concentrating on fractals when he was asked to look into a problem that IBM was having. What did the problem concern?

the increases in bugs as programs grew longer
noise in incoming signal transmissions
the errors in language translation algorithms
the heat produced by large mainframe computers

Answer:

noise in incoming signal transmissions

Mandelbrot graphed the noise rate and noticed that the graphs looked almost identical regardless of the time scale. It reminded him of the self similarity that he’d heard about with “the monsters.”

5. Which is these commonly used consumer devices makes applied use of fractals?

DVD players
cellular phones
microwave ovens
digital calculators

Answer:

cellular phones

Most cellular phones use antennas that are based on fractal designs. The recursive nature of self-similarity that is required of fractal values pretty much guarantee a wide variety of effective lengths meaning that they can handle a wide spectrum of signal frequencies in a smaller footprint than other antenna designs.

6. In 1904 one of the earliest and the most simple fractals was described by Helge von Koch, the “Koch Snowflake.”

This snowflake is based on what standard geometric shape?

a circle
a tesseract
a square
an equilateral triangle

Answer:

an equilateral triangle

To construct a Koch snowflake, you will need to do the following:

1) Start with an equilateral triangle.

2)Now divide each of the legs of that triangle into three equal parts and replace the middle third with two line segments of that length that form their own equilateral triangles (with no base), pointing outwards from the original shape.
This should be a six pointed shape similar to “the Star of David.” Not that the perimeter of the resultant shape is 4/3rds the length of the original perimeter.

3) Dividing each of the resulting line segments into three parts and repeating
this process will yield a figure that has 18 points and begins to resemble a snowflake

4)The fourth iteration will yield a figure with 54 points, then 162, 486 and so on..

Each iteration yields a figure that has a perimeter 4/3s of the length of the previous figure and it quickly becomes apparent that, as iteration continues the perimeter will approach infinity even though the enclosed area remains finite.

7. A slightly more complex fractal starts with an upright equilateral triangle and divides it into four equilateral triangles by connecting the midpoints of the three sides forming an upside down interior equilateral triangle.

Recursively performing this process for every resultant triangle produces a drawing that begins to look like a gasket. What is this fractal figure called?

the Cat’s Cradle
a Rubik’s Cube
the Sierpinski Triangle
a strange attractor

Answer: the Sierpinski Triangle

The Sierpinski Triangle is also sometimes called the Sierpinski gasket or the Sierpinski sieve. It was first conceived by Wac³aw Sierpiñski in 1915. Though it’s clearest when started with an equilateral triangle, other starting shapes can be used in this transformation. Most modern cell phone antennas are based on one of these types of functions.

8. Which of the following is NOT a good example of how fractals appear in nature?

a. snowflakes
b. the branching pattern of trees
c. the stripes on a zebra
d. coastlines

Answer: the stripes on a zebra

The stripes on a zebra are basically regular and mirror the growth patterns of grasses. If viewed in closer detail they do not exhibit the “self similar” aspect of fractals.

Conversely, zooming in on snowflakes, coastlines and tree branches all yield images that exhibit similarities to their zoomed out images.

9. Applying a set rules recursively to a particular problem occurs in several brain teaser games. Diagramming the shortest and longest solutions will sometimes result in figures that look uncannily like on of the fractals we’ve discussed. Which popular puzzles are an exemplar of that?

1-15 Sliding Number puzzle
Gordian Knot Puzzle
Key in Bottle Puzzle
Tower of Hanoi puzzle

Answer:

Tower of Hanoi puzzle

In Tower of Hanoi puzzles the player must move disks from one rod to another one at a time subject to rules. In the standard version, each move must take only one disk from a stack and place it atop any other stack and no larger disk may be placed on top of a smaller disk.

In a full solution of this puzzle, each disk will move only half as often as the disk directly above it and plotting the movements by the height of the disk moved creates a fractal-like shape (although it would only be a true fractal for an infinite height puzzle).

10. Fractal based equations have been found useful in all of these applications but one. Which?

a. creating movie CGI effects
b. determining optimal pathing in highway traffic situations
c. determining the length of coastlines
d. modelling the human circulatory system

Answer: determining optimal pathing in highway traffic situations

Loren Carpenter of Pixar Studios used fractals on low speed computers to simulate mountain ranges when employed at the Boeing company and then again at Lucasfilm in developing the world’s first fully CGI sequence for a feature film, “Star Trek II: The Wrath of Khan”. Mandelbrot initially presented his work in a paper “How Long Is the Coast of Britain?.” Repeated branching as in tress, the placement of leaves in ferns, and blood vessels in the circulatory system have all been successfully modeled using fractal functions.

Highway traffic problems don’t involve the sames aspects of natural roughness in which fractals excel. They tend to be more related to probability.

Sources: PinterPandai, Britannica, Hidden Dimension, Sporcle

Photo credit: Johannes Rössel / Wikimedia Commons (Public Domain)

Photo description: Sierpinski carpet (to level 6), a fractal with a topological dimension of 1 and a Hausdorff dimension of 1.893.