Binomial Theorem
Newton’s binomial is a mathematical formula given by Isaac Newton to find the expansion of any integer power of a binomial. It is also called Newton’s binomial formula, or more simply binomial theorem.
Newton’s binomial formula is as follows: For all (a,b)∈K2 (with K the set of reals or complexes) and for all n∈N: (a+b)n=n∑k=0 (nk)akbn−k.
How to calculate a binomial theorem of Newton?
If a = b = 1, the binomial formula simply becomes… the expression of the powers of 2 (since the coefficients only multiply by 1). We also check it on this decidedly magical triangle. Take for example n = 6 and add the values in the row: 1 + 6 + 15 + 20 + 15 + 6 + 1 = 64 = 26.
Newton’s binomial is a mathematical formula given by Isaac Newton to find the expansion of any integer power of a binomial. It is also called Newton’s binomial formula, or more simply binomial formula.
In Algebra, a binomial expression contains two terms joined by either addition or subtraction sign. For instance, (x + y) and (2 – x) are examples of binomial expressions.
Sometimes, you may need to expand binomial expressions as shown below:
(a + b)0 = 1
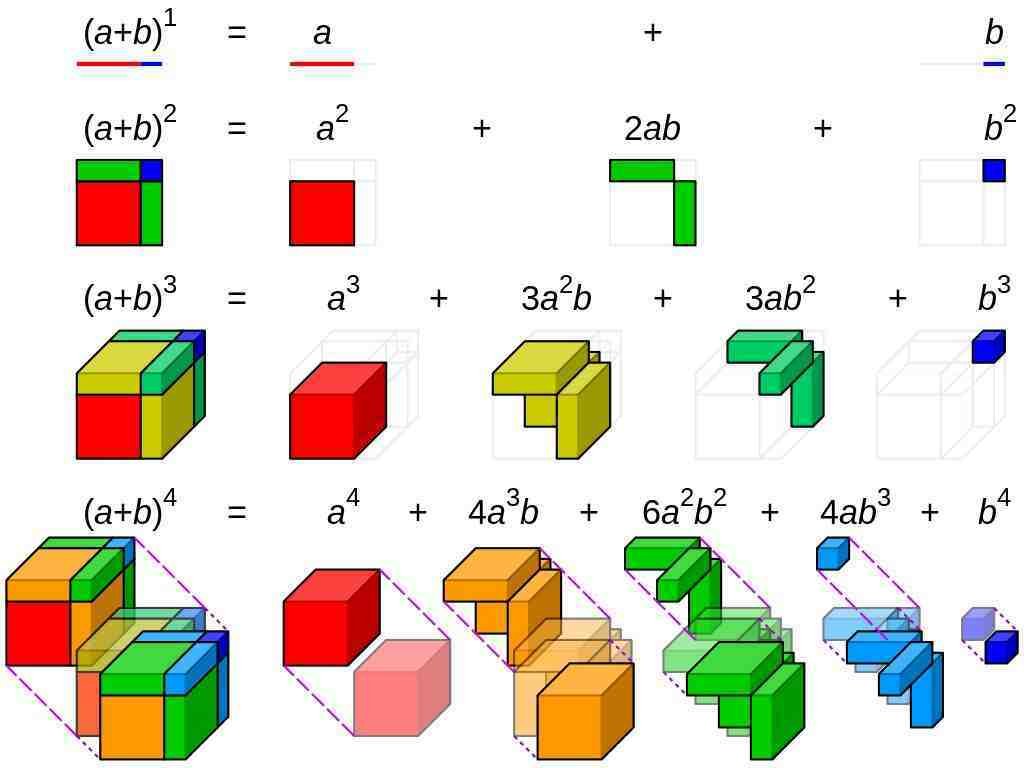
(a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
(a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
You realized that expanding a binomial expression by direct multiplication as shown above is quite cumbersome and inapplicable for larger exponents.
In this article, we will learn how to use the Binomial theorem to expand binomial expression without having to multiply everything out the long way.
Read also: Function Mathematics (f) | Understand and use the concept of function
What is the Binomial Theorem?
The binomial theorem were known to human beings since the 4th century BC. The binomial for cubes were used in the 6th century AD. An Indian mathematician, Halayudha, explains this method using Pascal’s triangle in the 10th century AD.
The clear statement of this theorem was stated in the 12th century. The mathematicians take these findings to the next stages till Sir Isaac Newton generalized the binomial theorem for all exponents in 1665.
The Binomial Theorem states the algebraic expansion of exponents of a binomial, which means it is possible to expand a polynomial (a + b) n into the multiple terms.
Mathematically speaking, this theorem is stated as:
(a + b) n = an + (n 1) an – 1b1 + (n 2) an – 2b2 + (n 3) an – 3b3 + ………+ b n
where (n 1), (n 2), … are the binomial coefficients.
Based on the above properties of the Binomial Theorem, we can derive the Binomial Formula as:
(a + b) n = an + nan – 1b1 + [n (n – 1)/2!] an – 2b2 + [n (n – 1) (n – 2)/ 3!]an – 3b3 + ………+ b n
Alternatively, we can express the Binomial formula as:
(a + b) n = nC0 an + nC1 an – 1b + nC2 an – 2b2 + nC3 an – 3b3+ ………. + n C n b n
Where (n r) = n Cr = n! / {r! (n – r)!} and (C) and (!) are the combinations and factorial respectively.
For example:
- 3! = (3)(2)(1) =6
- 5! = (5)(4)(3)(2)(1) =120
- 4! /2! = (4)(3)(2)(1)/(2)(1) =12
- 10C6 = 10! / (10 – 6)! 6! = 10! / 4! 6! = (1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10) / 1 x 2 x 3 x 4 x 1 x 2 x 3 x 4 x 5 x 6 = 7 x 8 x 9 x 10 /1 x 2 x 3 x 4 = 7 x 3 x 10 = 210
How to use the Binomial Theorem?
There are a few things which you need to remember while applying the Binomial Theorem.
These are:
- The exponents of the first term (a) decreases from n to zero
- The exponents of the second term (b) increases from zero to n
- The sum of the exponents of a and b is equal to n.
- The coefficients of the first and last term are both 1.
Read also: Unit Circle Algebra and Trigonometry | With Examples, Questions and Answers
Example of questions and answers of Binomial Theorem
Example 1 : Expand the expression (√2 + 1)5 + (√2 − 1)5 using the Binomial formula.
Answer:
(x + y)5 + (x – y)5 = 2[5C0 x5 + 5C2 x3 y2 + 5C4 xy4]
= 2(x5 + 10 x3 y2 + 5xy4)
= (√2 + 1)5 + (√2 − 1)5 = 2[(√2)5 + 10(√2)3(1)2 + 5(√2) (1)4]
=58√2
Example 2: Expand (x + 2)6 using the Binomial Theorem.
Answer:
Given a = x;
b = 2 and n = 6
Substitute the values in binomial formula
(a + b) n = an + nan – 1b1 + [n (n – 1)/2!] an – 2b2 + [n (n – 1) (n – 2)/ 3!]an – 3b3 + ………+ b n
⟹ (x + 2) 6 = x6 + 6x5(2)1 + [(6)(5)/2!] (x4) (22) + [(6)(5)(4)/3!] (x3) (23) + [(6)(5)(4)(3)/4!] (x2) (24) + [(6)(5)(4)(3)(2)/5!] (x) (25) + (2)6
= x6 + 12x5 + 60x4 +160x3 + 240x2 + 192x + 64
Read also: Fractal Geometry (Mathematics) | Definition, Explanation and Examples
Example 3: Find the expansion of (2x − y)4
Answer:
(2x − y)4 = (2x) + (−y)4 = (2x)4 + 4(2x)3 (−y) + 6(2x)2(−y)2 + 4(2x) (−y)3+ (−y)4
= 16x4 − 32x3y + 24x2y2 − 8xy3 + y4
Example 4
Use the binomial theorem to expand (2x + 3)4
Answer:
By comparing with the binomial formula, we get,
a = 2x, b =3 and n = 4.
Substitute the values in the binomial formula.
⟹ (2x + 3) 4 = x4 + 4(2x)3(3) + [(4)(3)/2!] (2x)2 (3)2 + [(4)(3)(2)/4!] (2x) (3)3 + (3)4
= 16 x4 + 96x3 +216x2 + 216x + 81
Example 5: Use the Binomial Theorem to expand (2 + 3x)3
Answer:
By comparing with the Binomial formula,
a = 2; b = 3x and n = 3
⟹ (2 + 3x) 3 = 23 + (31) 22(3x)1 + (32) 2(3x)2 + (3x)3
= 8 + 36x + 54x2 + 27x3
Example 6: Expand (x2 + 2)6
Answer:
(x2 +2)6 = 6C0 (x2)6(2)0 + 6C1(x2)5(2)1 + 6C2(x2)4(2)2 + 6C3 (x2)3(2)3 + 6C4 (x2)2(2)4 + 6C5 (x2)1(2)5 + 6C6 (x2)0(2)6
= (1) (x12) (1) + (6) (x10) (2) + (15) (x8) (4) + (20) (x6) (8) + (15) (x4) (16) + (6) (x2) (32) + (1)(1) (64)
= x12 + 12 x10 + 60 x8 + 160 x6 + 240 x4 + 192 x2 + 64
Example 7: Expand (a + b)5
Answer:
⟹ (a + b) 5 = an + (51) a5– 1b1 + (5 2) a5 – 2b2 + (53) a5– 3b3 + (54) a5– 4b4 + b5
= a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
Example 8: combinatoric to prove this theorem
If we want to use a combinatoric proof to prove the theorem and on the terms and results of the translation (x+y)^n (x+y)^n and of the form xn – jy jx^n – jy^j for j = 0, 1,2, … ,nj = 0.1,2, … , n.
To calculate the number of terms of the form xn – jy^j xn – jy^j, first we need to choose (n-j) (n-j) xx and from nn factors.
Therefore the coefficient of xn-jy^ jx^n-jy^j is (nn-j) (n-jn) which is equivalent to (nj) (jn).
Below is an example of a solution to illustrate the theorem, namely:
Example: How many values are there in the coefficient of x^12 y^13 in the expansion (x+y)^25 ?
Answer:
Dari teorema binomial, nilai koefisien x^12 y^13 dapat dihitung dengan.
(25/13) = 25!/ 13! 12! = 5.200.300.
Example: How many values are there for the coefficient x^12 y^13 in the expansion (2x – 3y) 25 (2x-3y) 25 ?
Answer:
The first thing to remember is that the expression (2x-3y) 25 (2x-3y) 25 = (2x+(-3y)) 25 (2x + (-3y)) 25, based on this binomial theorem we get:
(2x + (-3y)) 25 = ∑j = 025 (25j) (2x) 25 – j(−3y)j
As a result, the coefficient x12y13x12y13 on the expansion (2x+(−3y)) 25 (2x + (−3y)) 25 and can be obtained by j = 13^j = 13, namely:
(25/13) 2^12 (−3)^13 = − 25!/13! 12! 2^12 3^13
Sources: PinterPandai, Cue Math, Math is Fun
Photo credit: Author: Cmglee (CC BY-SA 3.0) via Wikimedia Commons
Photo description: visualisation of binomial expansion up to the 4th power.