Golden Ratio φ mathematics
The golden ratio or golden number (also called God ‘s number, extreme and mean ratio) is an irrational number, represented by the Greek letter φ (phi) (lowercase) or Φ (Phi) (uppercase) after the Greek sculptor Phidias.
It is an irrational number, unique solution of the equation x² = x + 1. It is approximately 1.61803398875.
Formula
φ = (1 + √5) / 2
What is golden ratio?
Golden ratio is a proportion, initially defined in geometry as the unique ratio a/b between two lengths a and b such that the ratio of the sum a + b of the two lengths to the greater (a) is equal to that of the greater (a) on the smaller (b).

The golden ratio (phi) represented as a line divided into two segments a and b, such that the entire line is to the longer a segment as the a segment is to the shorter b segment. Traced by Stannered, Public domain, via Wikimedia Commons
The golden ratio in geometry
The first definition of the golden ratio is geometric.
The theorem is as follows: “Two lengths a and b (strictly positive) respect the “golden proportion” if the ratio of a to b is equal to the ratio of a + b to a.”
In the light of the works of Euclid, a new definition of the golden ratio appears:
“The golden ratio is the positive real number, noted φ, equal to the fraction a/b if a and b are two numbers in proportion of extreme and average ratio.”
Here is the corresponding formula: φ = (1 + √5) / 2.
φ is the solution of a quadratic equation, which allows us to give a third definition:
“The golden ratio is the unique solution of the equation x² – x – 1 = 0.”

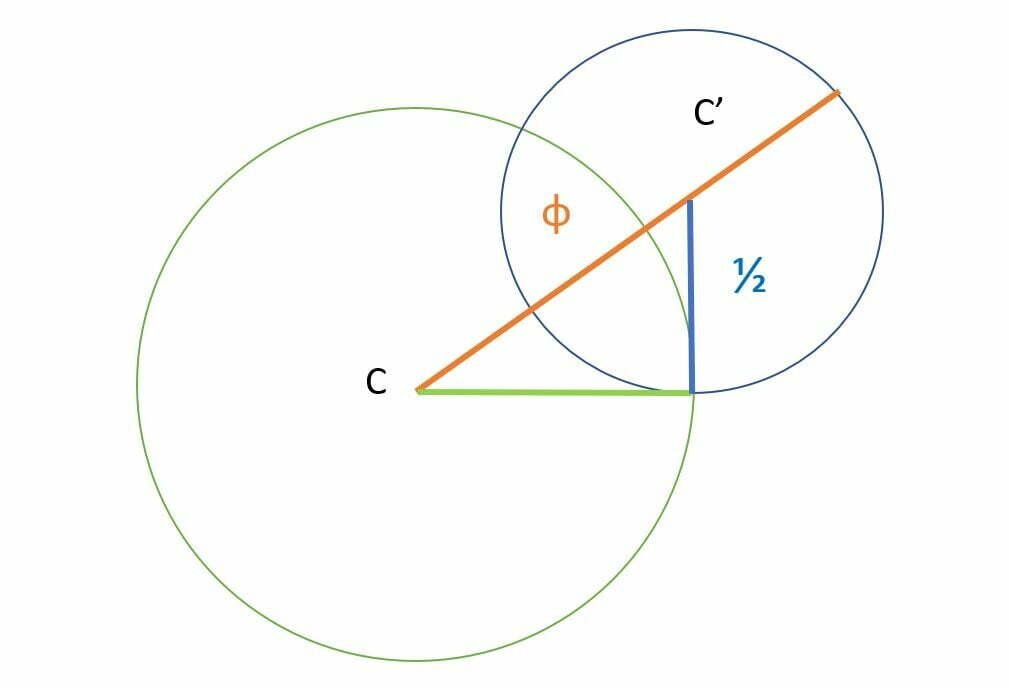
Thanks to these calculations, it is possible to draw a proportion of extreme and average reason using a compass, a ruler and a square:
- Draw a circle C of radius 1,
- At the end of ray 1, draw a segment of length 1/2, perpendicular to the ray,
- Draw the circle C’ of radius 1/2 by placing the point of the compass at the end of the segment of length 1/2 previously drawn,
- Draw the segment from the center of circle C to the end of circle C’ passing through the center of circle C’,
- The length of this segment is the golden ratio.
From these circles, it is possible to build a golden rectangle.
We can also integrate a square of side a − b into the golden rectangle of side b × (a − b). By adding a quarter circle in each square, we obtain a spiral, called the golden spiral.
The golden ratio can also be used for the construction of pentagons and pentagrams and also in trigonometry.

Leonardo da Vinci’s Vitruvian Man respects the proportions explained by Vitruvius, rational preferred to the golden ratio by Pacioli as far as works of art are concerned. Leonardo da Vinci, Public domain, via Wikimedia Commons. If you spread your legs wide enough so that your height decreases by a fourteenth, and if you open and raise your arms so that the middle fingers are level with the top of the head, know that the navel will be in the middle between the ends of the limbs apart and your legs apart will form two sides of an equilateral triangle. Leonardo da Vinci was fascinated by the human body and the physical mechanisms it contains, but both in the spirit of Vitruvius and in that of Leonardo Da Vinci, this representation of man is purely artistic, not at all scientific.
The golden number in arithmetic
The other method of defining the golden ratio is algebraic.
In algebra, the golden ratio is defined as the unique positive root of an equation.
By using both approaches, algebraic and geometric, it is possible to solve a quadratic equation. We then speak of geometric algebra. φ² = 1 + φ has the golden ratio as its solution.
The golden ratio can also be approximated using the continued fraction at infinity. 1 + (1/(1 + (1/1))).
The Fibonacci sequence also provides approximations of the golden ratio:
F(n) = (x^n – (1-x)^n)/(x – (1-x)) where x = (1+sqrt 5)/2 ~ 1.618. Therefore, phi = 0.618 and 1/Phi.
And conversely, Binet’s formula expresses the Fibonacci sequence as a function of the golden number.
The golden section is also used in some Diophantine equations.
Ratios of consecutive, Fibonacci numbers
| deviation to φ in % | |||
|---|---|---|---|
| 1 | 1 | = 1.0000 | −38 |
| 1 | 2 | = 2.0000 | +23 |
| 2 | 3 | = 1.5000 | −7.3 |
| 3 | 5 | ≈ 1.6667 | +3.0 |
| 5 | 8 | = 1.6000 | −1.1 |
| 8 | 13 | = 1.6250 | +0.43 |
| 13 | 21 | ≈ 1.6154 | −0.16 |
| 21 | 34 | ≈ 1.6190 | +0.063 |
| 34 | 55 | ≈ 1.6176 | −0.024 |
| 55 | 89 | ≈ 1.6182 | +0.0091 |
| 89 | 144 | ≈ 1.6180 | − 0.0035 |
| 144 | 233 | ≈ 1.6181 | +0.0013 |
What is the relationship between the golden ratio and the Fibonacci sequence?
There is a special relationship between the golden ratio (1.618…) and the Fibonacci sequence (0, 1, 1, 2, 3, 5, 8, 13, 21 etc…) in which each number is the sum of the two numbers preceding it.
When we take two consecutive numbers in the Fibonacci sequence, and divide the larger by the smaller, the result is very close to the golden ratio. The higher the numbers of the Fibonacci sequence, the closer the result is to the Golden Ratio. In other words, the Golden ratio appears by dividing any number of the Fibonacci sequence by its predecessor. The larger the numbers, the more accurate the approximation.
Take for example two high numbers following each other in the Fibonacci sequence and divide the larger by the smaller:
10946 divided by 6765 = 1,6180339985218033…
———————————–
———————————–
How is the Fibonacci sequence constructed?
The first two numbers are 0 and 1, and then each successive number is the sum of the two numbers before it: 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, etc…
——-
What is the Golden Spiral?
The Golden Spiral is a direct derivative of the Golden Ratio, a geometric shape derived directly from divine proportions. It is made up of quadrants inscribed in each square.

Golden spirals are self-similar. The shape is infinitely repeated when magnified. Jahobr, CC0, via Wikimedia Commons
——-
What is the Golden Angle?
The golden angle is 137.5 degrees.
The Golden Angle arises when a circle is divided into two sections whose two lengths are in a ratio equal to the golden ratio.

The golden angle is the angle subtended by the smaller b (red) arc when two arcs that make up a circle are in the golden ratio. Or a/b= φ (φ being the golden number). User:Dicklyon, Public domain, via Wikimedia Commons
Sources: PinterPandai, MathIsFun, Wolfram, CueMath
Fibonacci number denoted as Fn | Examples, questions and answers