Alternating Current (AC): Definition, Formula, RMS, Power, Phasors, and Transformers
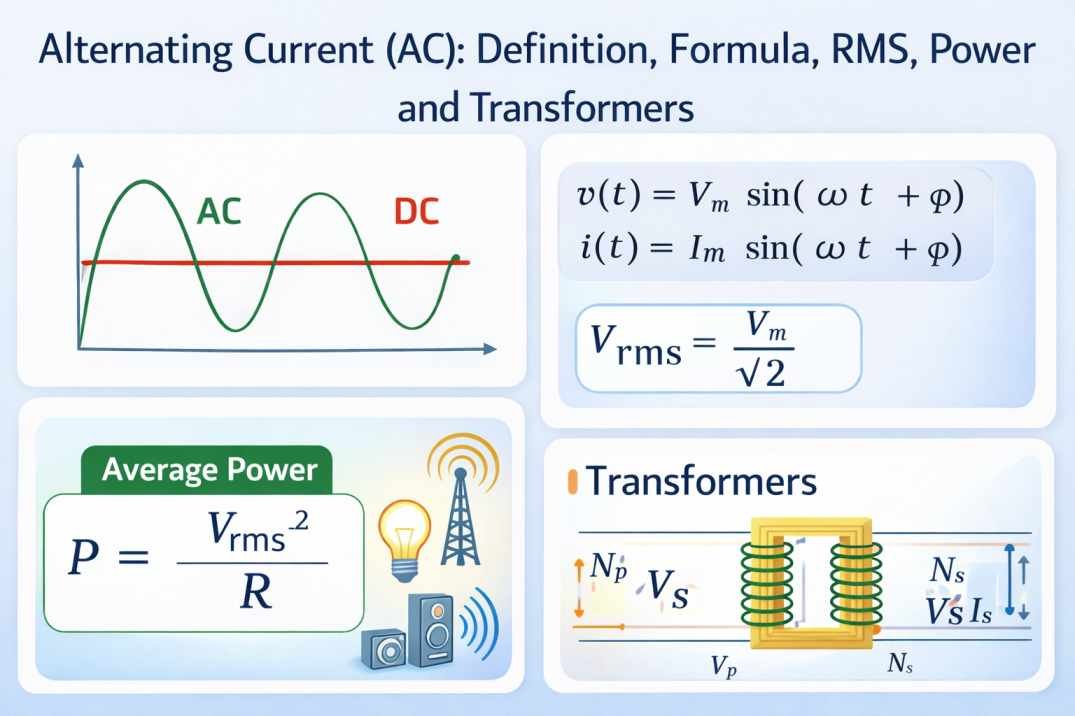
Alternating current (AC) is an electric current in which both the magnitude and direction change periodically over time.
This is fundamentally different from direct current (DC), where electric charge flows in only one direction.
Most electrical power used in homes, offices, and industries worldwide is delivered as AC electricity because it can be transmitted efficiently over long distances and easily transformed to higher or lower voltages.
In standard power systems, alternating current usually has a sinusoidal waveform.
However, in electronics and signal processing, other waveforms such as square waves and triangular waves are also commonly used.
1. Basic Formula of Alternating Current
For a sinusoidal alternating current, the instantaneous voltage and current are expressed mathematically as:
v(t) = Vm sin(ωt + φ)
i(t) = Im sin(ωt + φ)
Where angular frequency and period are defined as:
ω = 2πf
f = 1 / T
Explanation of Symbols
| Symbol | Meaning | Unit |
|---|---|---|
| v(t) | Instantaneous voltage | Volt (V) |
| i(t) | Instantaneous current | Ampere (A) |
| Vm, Im | Peak (maximum) value | V, A |
| ω | Angular frequency | rad/s |
| f | Frequency | Hz |
| T | Period | Second (s) |
| φ | Phase angle | rad / degree |
2. Peak-to-Peak Voltage
The peak-to-peak voltage is the total voltage swing from the maximum positive peak to the maximum negative peak:
Vpp = 2Vm
3. Power in AC Circuits
For a purely resistive AC circuit, instantaneous power is:
p(t) = v(t) · i(t)
p(t) = v(t)2 / R
In practice, engineers use average power, calculated using RMS values:
Average AC Power
P = Vrms2 / R
4. Root Mean Square (RMS)
Root Mean Square (RMS) represents the effective value of AC voltage or current.
It is the equivalent DC value that would produce the same heating effect in a resistor.
Vrms = √( (1/T) ∫0T [v(t)]² dt )
RMS for Common Waveforms
- Sinusoidal:
Vrms = Vm / √2 - Triangular:
Vrms = Vm / √3 - Square:
Vrms = Vm
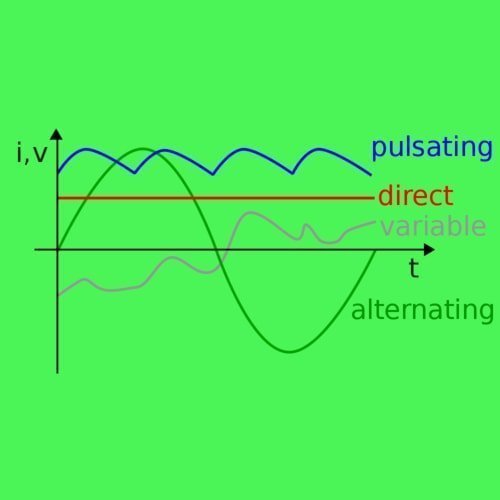
Alternating current (green) vs direct current (red). Source: Wikimedia Commons
5. Phasors and Phase Angle
AC quantities are often analyzed using phasor diagrams.
A phasor is a rotating vector that simplifies calculations involving phase differences.
- The phasor length represents the maximum value.
- The projection represents the instantaneous value.
- Phasors are mathematical tools (AC voltage and current are scalar quantities).
6. Transformers and Why AC Is Used for Power Transmission
A transformer transfers electrical energy between circuits using electromagnetic induction.
Transformers work only with alternating current, which is why AC dominates large-scale power transmission.

Transformer Voltage Relationship
Vp / Vs = Np / Ns
VpIp ≈ VsIs
This shows that voltage transformation depends on the number of turns in each coil.
7. Real-World Applications of Alternating Current
- Residential and commercial electricity supply
- Audio signals and amplifiers
- Radio-frequency communication
- Industrial motors and generators
Trusted References
- PinterPandai
- Wikipedia – Alternating Current
- OpenStax University Physics Vol. 2
- Khan Academy – AC Circuits
- CleverlySmart – Science Explained Clearly
Educational content only. Not a substitute for professional electrical engineering advice.